GammaSwap Protocol

Introduction

In a previous article, I wrote about the similarity of liquidity provision in automated market makers such as Uniswap to the short straddle option strategy in traditional financial markets.

In a follow up article, I explained that the lack of an ability to go long volatility/gamma through automated market makers created periods of too much downward pressure on the price of volatility through AMMs like Uniswap. This results in a market inefficiency where liquidity providers are not being fairly compensated for the risk they take when they provide liquidity. A problem that over time will have negative effects on available liquidity in decentralized exchanges.

In this article, I will introduce the GammaSwap protocol — a protocol for going long gamma through constant function market makers (CFMMs) such as Uniswap, Sushiswap, Balancer, etc. GammaSwap enables users to purchase not just long straddles but also expose oneself to payoff functions that are similar to those of call and put options.

As a side benefit the protocol also allows for the possibility of a fee-less DEX.

Selling Volatility/Short Gamma

The GammaSwap protocol cannot function without the existence of volatility sellers. That is liquidity providers to CFMMs.

Liquidity providers will provide liquidity to CFMMs just as they currently do with the distinction that they’ll provide it through GammaSwap. That is, LPs will send their tokens to GammaSwap which will deposit them into a CFMM (e.g. Uniswap, Pancakeswap, etc.) in exchange for LP tokens.

These LP tokens from other CFMMs, however, will not be provided to the liquidity provider. Instead, they will remain in GammaSwap. GammaSwap will issue its own GammaSwap liquidity pool tokens, identical to the liquidity pool tokens in CFMMs such as Uniswap issue (e.g. ERC-20 tokens), that represent a liquidity provider’s stake in the CFMM’s liquidity pool.

When liquidity providers seek to retrieve their deposited liquidity, they will exchange the GammaSwap liquidity pool tokens for the reserve tokens. To do this, GammaSwap measures their representation in the CFMM’s liquidity pool tokens, then burns the tokens and uses the CFMM’s liquidity pool tokens to retrieve the tokens the liquidity provider deposited.

The accrued fees from the AMM pool that GammaSwap is wrapping will accrue to the GammaSwap liquidity provider along with the additional borrow rate paid by those borrowing LP tokens.

The incentive to provide liquidity on GammaSwap is that you will earn a boosted yield from your LP positions. The only additional risk is the additional smart contract risk.

The mechanics of how this process represents a short gamma position have been covered extensively in a previous article. Therefore, I will just post the return function of providing liquidity through GammaSwap assuming assets provided as liquidity were borrowed and therefore hedged.

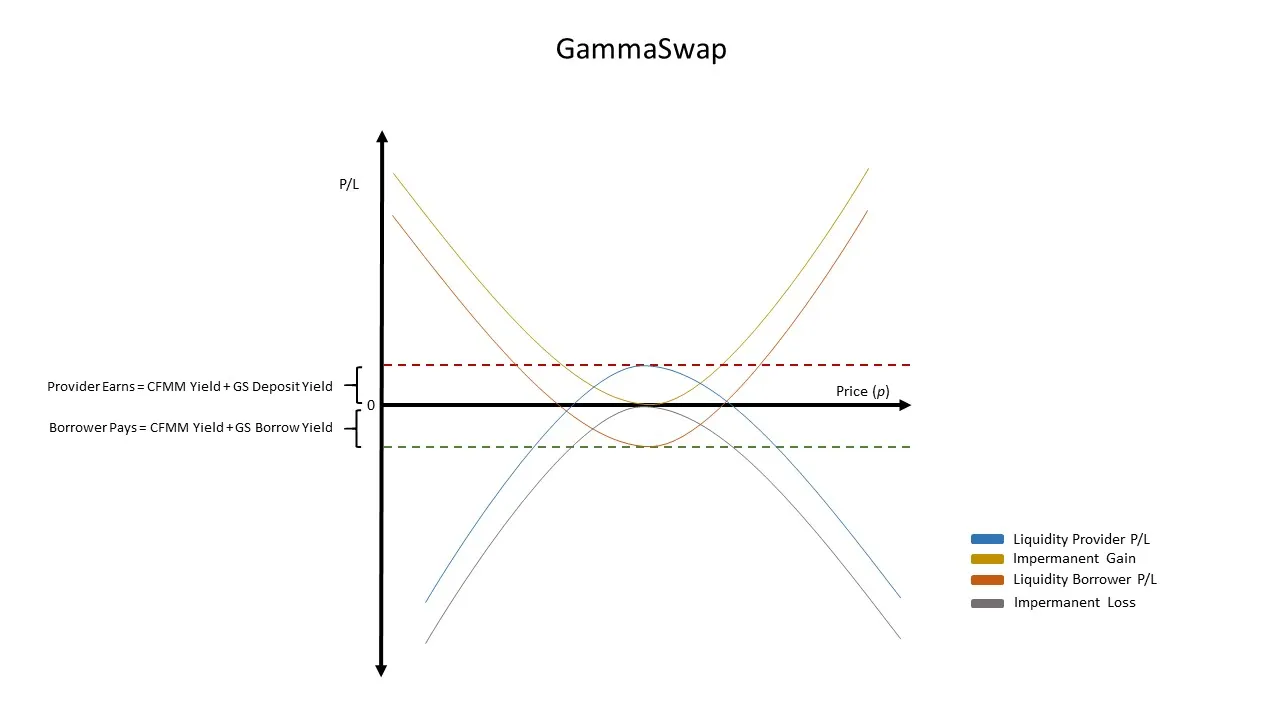
A graphical representation of the return function of providing liquidity through GammaSwap assuming assets provided as liquidity were borrowed is below. For comparison I added the returns of providing liquidity to the CFMM outside of GammaSwap.

At any point in time a liquidity provider providing liquidity through GammaSwap will have outperformed providing liquidity directly through the CFMM.

Buying Volatility/Long Gamma

If providing liquidity to a CFMM accomplishes a short gamma position, then buying short liquidity from a CFMM would accomplish a long gamma position. CFMM liquidity can be shorted by borrowing liquidity from the CFMM and withdrawing the reserve tokens it represents and holding them, such that the impermanent loss becomes an impermanent gain. The impermanent gain is the ability of the borrower to purchase more LP tokens with their reserve tokens.

The borrower of course will also owe the trading fees that accrue on the liquidity borrowed. All variables are the same as the previous function.

The graphical representation of this return function is the following The r variable would be the interest at which the withdrawn reserve tokens are lent to earn a yield that would reduce the cost from the yield from trading fees in a CFMM.

Unfortunately, CFMM platforms do not allow the borrowing of liquidity. This is what differentiates GammaSwap from other liquidity provisioning platforms.

The GammaSwap protocol aggregates liquidity tokens from popular CFMMs such as Uniswap, Pancakeswap, Sushiswap, etc., to allow them to be lent to other users who wish to achieve a long gamma exposure.

The GammaSwap protocol lends liquidity deposited into CFMMs by withdrawing the reserve tokens and holding them inside the GammaSwap smart contract as collateral. GammaSwap keeps track of the ratio of reserve tokens withdrawn, and the price of the tokens at the time the borrower acquired her loan. The impermanent loss that lenders experience will become an impermanent gain to borrowers of liquidity. In exchange, liquidity borrowers will owe an interest on the liquidity they borrowed plus the trading fees that accrued to the liquidity in the CFMM.

Since the growth of the liquidity token debt can become greater than the reserve tokens of the liquidity she withdrew, liquidity borrowers will have to over collateralize their loans to ensure there is enough funds to acquire the liquidity tokens and pay the accrued yield from trading fees and interest to liquidity providers.

The process of opening a long gamma position is described as follows, The borrower of liquidity receives an NFT (ERC-721) with which he can identify his long gamma position in the GammaSwap smart contract.

Since the impermanent loss to LPs becomes the impermanent gain of the borrower, the borrower will have achieved a long gamma position whose return can be characterized by the following function The variable g_b is the interest rate GammaSwap charges liquidity borrowers for borrowing liquidity from the platform. All other variables are the same as the previous function.

A graphical representation of the above function is as follows Although there is the potential to lend the reserve tokens from the withdrawn liquidity at r, most likely that will not be possible without having adequate risk measures. Therefore, r will most likely be 0.

Since borrowed liquidity will not be inside the CFMM, it will not be accruing trading fees from the CFMM.

For that reason, GammaSwap will keep track of the trading fees from the CFMM accrued to a loan using the following function x and y are the reserve assets, L is the invariant, which is the geometric mean of the reserve assets in a CFMM like Uniswap. LP_Shares is the number of liquidity pool shares in the CFMM. The formula for the return from trading fees in the CFMM is essentially the growth of the invariant divided by the growth of the liquidity pool shares.

GammaSwap is able to keep track of the yield accruing to liquidity providers by treating loans in terms of the invariant it represents inside a CFMM, rather than as LP shares.

The yield LPs earn inside a CFMM is the growth in the invariant, which is the geometric mean of the reserves in platforms such as Uniswap, not the change in LP shares.

Therefore all interest owed by borrowers and paid to lenders is kept track of in the form of additional invariant units from the CFMM.

Accrued interest the borrower owes will be tracked through an ever increasing index inside GammaSwap whose rate of growth will change based on the utilization rate of the pool. This rate of growth represent the actual interest being charged to borrowers. Since the utilization rate is always less than one, the lending yield that is paid to depositors (liquidity providers) is always lower than the borrowing yield.

From the above functions, one can can derive functions to calculate the total amount charged to borrowers and paid to lenders of the pool at any given time. Those functions are as follows

Therefore. as available liquidity to borrow dries up through the utilization rate approaching one, the interest will rise in the platform which will incentivize LP to provide liquidity through GammaSwap.

Conversely as it falls, it will incentivize borrowers to short liquidity through GammaSwap.

Every liquidity loan will also keep track of the block in the Ethereum blockchain at which it was opened, the number of the GammaSwap borrow index at which it was started and the liquidity borrowed, the interest accrued to a borrower will always be easily calculated through the following formula

When a liquidity borrower is ready to close his position, he simply nets the position.

The liquidity borrower will have either lost collateral or gained reserve tokens depending on the price delta of the token pair in the CFMM minus the trading fees and GammaSwap interest paid to LPs.

The process of closing the loan is the following

The borrower initiates a closing position in GammaSwap. The smart contract calculates the LP tokens with accrued interest the loan represents and deposits enough reserve tokens into the CFMM to receive those LP Tokens to pay back to liquidity providers. The borrower then receives whatever is left of her collateral plus the impermanent gain she made on price variation minus the interest she owed from trading fees accrued to the CFMM and interest owed to liquidity providers.

The result is a market where borrowers of liquidity pool shares pay the CFMM trading fee yield plus the GammaSwap borrow yield and liquidity providers receive the CFMM trading fee yield plus the GammaSwap lending yield.

Calls and Puts

The GammaSwap protocol does not just create the opportunity to purchase straddles but also to customize the volatility exposure to approximate the returns of a call or put option. This is achieved by changing the ratio of tokens held as collateral within GammaSwap, that essentially changes the payoff function of the impermanent gain.

For example, suppose a gamma buyer decides to swap delta units of token x for token y, such that the ratio of reserve tokens held as collateral from the liquidity borrowed is now different from the one she held at the beginning of the loan.

Her return function will now be the following g is the GammaSwap borrow rate.

So one can either lean the ratio more to one token or the other and obtain a return function that is similar to traditional call or put options.

As you may have noticed the amount required to be deposited as collateral in both situations increases substantially. This is necessary to make the position impervious to flash loan attacks. However, such positions can be financed through loans on decentralized lending platforms such as Aave or Compound.

The formula for the price at which the position’s loss is maximized (the max loss price) is given below

The liquidity that collateral tokens represent at any point in time is given by the following formula

Since the liquidity borrowed is constant and only grows with the trading fees and GammaSwap borrow yield, we can use the formula above to see what liquidity the collateral can provide at the max loss price (p_max)

One would therefore need to add additional collateral in terms of token x and y to make sure that the position will remain over collateralized over the required maintenance threshold at the p_max price.

What you essentially receive by changing the ratio of the reserve tokens used as collateral is a perpetual long volatility position that benefits more from a single sided directional move in the market. This is similar to what you could achieve with a call or put option. However, the added benefit is that if the price were to move too far against you, you might still have a gain.

Of course, if one were to use GammaSwap with a CFMM like Balancer, where the reserve tokens are already weighted to one side, the benefit of a higher delta (rate of change in the value of the position due to the change in the underlying price) as price moves in one direction would be more pronounced.

Ensuring Safety of Deposits

Since there’s the potential for loans to become undercollateralized if trading fees plus interest accrued surpass the amount of collateral deposited to open a long gamma position, there will be an incentive to liquidate loans.

That is, a gamma buyer will be required to deposit collateral beyond a certain threshold and maintain that collateral above a certain threshold or face liquidation through a third party who will be compensated with a percentage of the collateral.

To do this, the GammaSwap protocol will emit events detailing information about a loan that can be read by liquidation bots keeping track of the health of the loans constantly checking the Ethereum blockchain.

No Dependency on Oracles

Lending platforms typically depend on oracles to ensure the safety of assets. A problem that diminishes the amount of assets available for lending due to the lack of robust oracles for every asset.

Unfortunately, these platforms must depend on oracles because depending on CFMMs for pricing data leaves them vulnerable to flash loan attacks where the price of collateral can be momentarily depressed enough to force liquidations on an otherwise healthy loan.

Fortunately for GammaSwap, due to the shape of its payoff curve, price manipulation through flash loans will never drop the value of collateral to zero. The value of that collateral can always be dropped to a minimum (in addition to extra collateral to cover the trading fee yield and interest) required by all volatility buyers to maintain in order to have a position open.

This opens the possibility for GammaSwap to not just provide long gamma exposure to a small number of token pairs but rather to the entire crypto space without dependency from a third party for price verification, as is the case of Aave and Compound.

Hence, even brand new untested projects can offer long volatility exposure to increase the yields to liquidity providers in its tokens and to lower the risk of participating in such projects.

Although, given the current implementation of CFMMs, it is possible for an attacker to do enough round trips (buying and selling paying a small fee, typically 0.6%, per round trip) on a CFMM to make the yield from trading fees spike high enough to force liquidations on some positions, it is highly unlikely given the cost it would entail to design this malicious attack.

Nevertheless, we have systems in place to safe guard against such attacks in our platform.

Fee-less Trading of Tokens

The entire yield paid to liquidity providers is made up of trading fees plus interest with GammaSwap providing the pricing function for the interest.

One can imagine that if GammaSwap were using another CFMM for the same token pair that did not charge trading fees to its users, the total GammaSwap yield would be at least be about as high as that of the CFMM that does charge trading fees.

Since GammaSwap makes it possible to purchase and sell volatility, in the event that GammaSwap yields were significantly lower than other CFMM’s, there would be an arbitrage opportunity.

Hence there is no need for CFMMs leveraging our model to charge trading fees to its users. The traders role in GammaSwap is not to pay liquidity providers for the risk they expose themselves to but rather to net the positions of gamma buyers who are the actual buyers of the risk liquidity providers are selling.

A two sided marketplace of volatility will be more efficient than a market place that sells volatility for volume, like in a traditional AMM.

Liquidity borrowers pay liquidity providers the GammaSwap borrow yield. Hence there’s no need for token traders to pay commissions to liquidity providers. Their role instead is to update the positions of buyers and sellers of volatility in exchange for the facilitation of their trades. The difference in the borrow and deposit yield is the bid/ask of the price of volatility. A spread that is found in all markets.

Hence, since LPs do not need to be compensated through the risk they take using fees, a fee-less DEX can be operated using GammaSwap. Gamma sellers earn their revenue from gamma buyers, while using spot buyers and sellers, who trade commission free, to net their positions against gamma buyers.

The incentive for spot traders to net the positions of gamma traders in GammaSwap, besides the zero commission trades and facilitation of their transactions, is the arbitrage opportunities against other exchanges whose prices for reserve tokens differ from GammaSwap.

Conclusion

In this article I described the GammaSwap protocol. A protocol to enable the trading of volatility through perpetual derivative instruments that resemble straddles, calls, and puts in traditional financial markets.

These new types of derivative products have never existed before. They are perpetual and netted through a floating swap rate that is determined by market forces. An added benefit of them is their ability to enable commission free trading of any token pair. The hope of this project is to correct mispricings in current decentralized volatility markets to support the growth of liquidity in decentralized finance and therefore ensure that the future of finance is decentralized.

Register on our website to be notified when the platform is launched.